Hi Zusammen,
ich mache diesen neuen Thread auf, um mit Mathias (masi) und allen anderen Interessierten über die Themen zu diskutieren, die in meinem Papier Understanding Image Sharpness angesprochen werden.
Das Papier findet sich hier:
http://www.falklumo.com/lumolabs/articles/sharpness/index.html
Der englische Threadtitel soll Zufallsbesucher abhalten, denn hier geht es nicht um Bildkunst
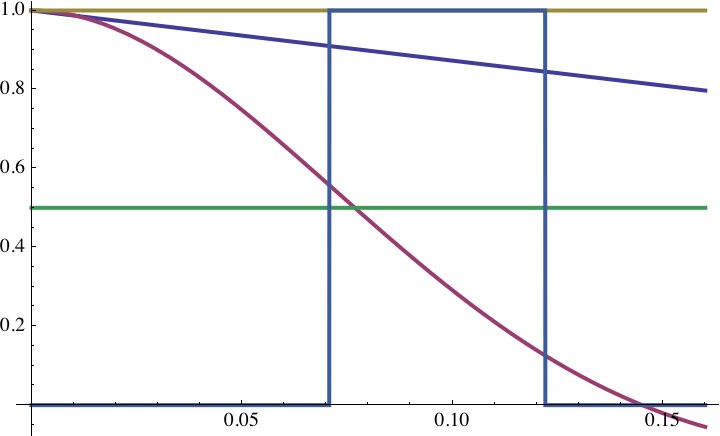
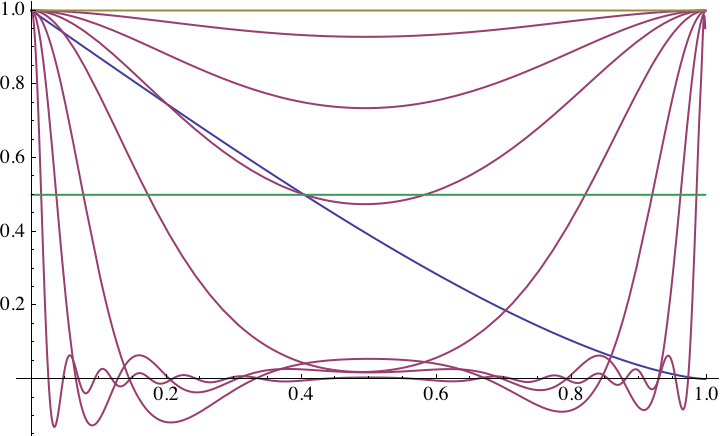
Den Anfang soll die laufende Diskussion machen, welche Blurbreite den Effekt der Defokussierung am treffendsten charakterisiert, also in etwa MTF50 der Defocus-MTF entspricht. Und wie sich diese Unschärfe verrechnet.
Eine erste Referenz findet sich hier:
http://spie.org/x32396.xml
Offensichtlich wird das Thema wellenoptisch beackert, mit einer OPD = ~ delta/8N^2
Das könnte sogar ungefähr hinkommen, denn mit delta=60micron Fokusungenauigkeit (einem Wert, den ich öfter messe) und N=4 komme ich dann auf 0.48 micron OPD oder 0.85 Lambda.
Dafür finden sich wiederum hier Formeln:
http://www2.ensc.sfu.ca/~glennc/e376/e376l20a.pdf
ich mache diesen neuen Thread auf, um mit Mathias (masi) und allen anderen Interessierten über die Themen zu diskutieren, die in meinem Papier Understanding Image Sharpness angesprochen werden.
Das Papier findet sich hier:
http://www.falklumo.com/lumolabs/articles/sharpness/index.html
Der englische Threadtitel soll Zufallsbesucher abhalten, denn hier geht es nicht um Bildkunst
Den Anfang soll die laufende Diskussion machen, welche Blurbreite den Effekt der Defokussierung am treffendsten charakterisiert, also in etwa MTF50 der Defocus-MTF entspricht. Und wie sich diese Unschärfe verrechnet.
Eine erste Referenz findet sich hier:
http://spie.org/x32396.xml
Offensichtlich wird das Thema wellenoptisch beackert, mit einer OPD = ~ delta/8N^2
Das könnte sogar ungefähr hinkommen, denn mit delta=60micron Fokusungenauigkeit (einem Wert, den ich öfter messe) und N=4 komme ich dann auf 0.48 micron OPD oder 0.85 Lambda.
Dafür finden sich wiederum hier Formeln:
http://www2.ensc.sfu.ca/~glennc/e376/e376l20a.pdf